【統計】平均値、中央値、最頻値・・・データの中心を説明する指標
データの中心を説明する指標を説明します。よく用いられる指標として平均、中央値、最頻値があります。これらはデータを代表する値として使われることが多いです。
10人の生徒のテストの点数が下表の時、平均、中央値、最頻値はいくつになるでしょうか?
| 生徒 | Aさん | Bさん | Cさん | Dさん | Eさん | Fさん | Gさん | Hさん | Iさん | Jさん |
| 点数 | 30 | 40 | 40 | 50 | 60 | 70 | 70 | 70 | 80 | 100 |
平均
データの中心として最もよく知られているものは平均です。単に平均と言っても、算術平均、加重平均、幾何平均、調和平均などがありますが、その中でも算術平均が良く使われ、単に平均ということが多いです。
(加重平均、幾何平均、調和平均については別途説明します)
平均値は値の和をデータ数で割ったものです。
平均値$\overline{X}=\cfrac{X_{1}+X_{2}+\cdot\cdot\cdot+X_{n}}{n}$
(観測値:$X_{1}+X_{2}+\cdot\cdot\cdot+X_{n}$, データの大きさ:$n$)
冒頭の10人の生徒の点数の平均値は、
$\overline{X}=\cfrac{10人の点数の合計}{10人}=\cfrac{30+40+40+50+60+70+70+70+80+100}{10}=61点$
中央値
中央値は、メディアンmedian、中位数として知られています。
データを小さい順(大きい順でもOK)で並び替えたときの中央の値です。
データが小さい順に$X_{1}+X_{2}+\cdot\cdot\cdot+X_{n}$ と書くとき、
データの大きさが奇数(n=2m+1)の場合、中央値はm+1番目$X_{m+1}$ となります。
データの大きさが偶数(n=2m)の場合、中央値はm番目とm+1番目の平均 $(X_{m}+X_{m+1})/2$ となります。
冒頭の10人のテスト結果はn=10(偶数)なので、中央値は5番目と6番目の平均となります。中央値は70点と60点の平均で、80点となります。
最頻値
平均値、中央値のほかによく使われる指標として最頻値があります。モードmodeともいわれます。
データの中で最も頻繁に出現する値を示します。冒頭のの10人のテスト結果では70点が3人で最も出現していますので、70点が最頻値となります。
| 平均値 | 中央値 | 最頻値 |
| 61 | 65 | 70 |
平均値、中央値、最頻値の使い分け
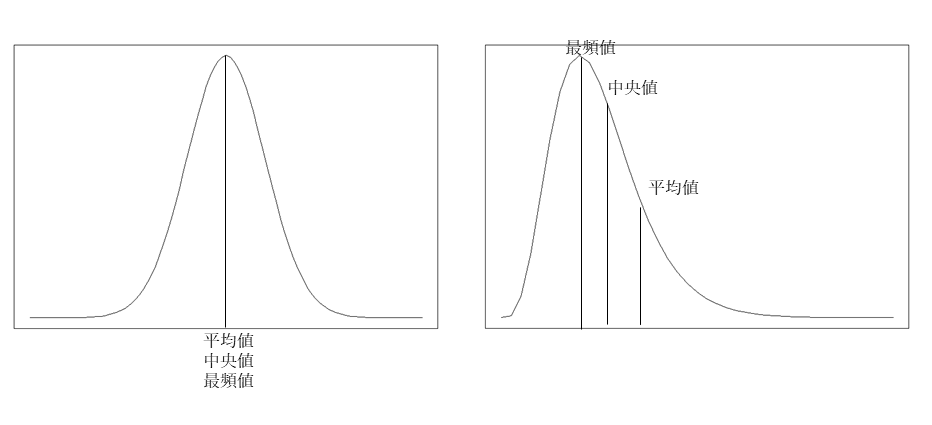
平均値、中央値、最頻値の関係は、正規分布のように左右対称の分布の場合、この3つは完全に一致します。
左右対称ではなく、左に寄った分布(右に裾が長い分布)の場合、一般に平均、中央値、最頻値の順に大きくなります。
分布がほぼ左右対称の場合は、どれを使っても大して変わりません。歪んだ分布であるとか、極端な外れ値があるデータ出ない限りは平均を使うのが良いと考えます。問題は歪んだ分布の場合にどれを選ぶかです。一般に外れ値に引っ張られないという点で中央値が良いといわれています。 代表値の使い分けは状況に応じて考える必要があり、平均値で良いのか、中央値の方がデータの意味を捉えているのか適切に判断することが大切です。